Titrationskurve berechnen
Eine an sich einfach klingende Aufgabe, mit der ich letztens in meinem Chemiekurs kläglich gescheitert bin – es war zu früh, es war nicht gut vorbereitet, ich habe den Anspruch der Aufgabe einfach unterschätzt:
Aufgabe:
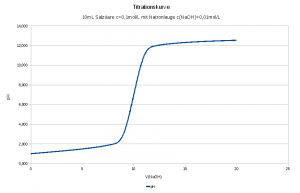
Berechnen Sie die Titrationskurve der Titration von 10mL Salzsäure der Konzentration c(HCl)=0,1mol/L mit 20mL Natronlauge der Konzentration von c(NaOH)=0,1mol/L. Stellen Sie dazu den pH-Wert der Lösung in Abhängigkeit vom zugegebenen Volumen an Natronlauge dar.
Vorüberlegungen:
Zwei Punkte der Titrationskurve sind relativ einfach zu finden:
- Zu Anfang der Titration (0mL Zugabe von Natronlauge) muss der pH-Wert 1 betragen, da ja gilt: pH=-1*lg(c(H3O+))=-1*lg(0,1)=1
- Definitionsgemäß ist am Aquivalenzpunkt – also nach Zugabe von 10mL Maßlösung – ein pH-Wert von 7 erreicht, da ja gilt pKw=pH+pOH=14; c(OH-)=c(H3O+) am Äquivalenzpunkt (grün), da alle zusätzlichen Hydroniumionen aus der Protolyse der Säure neutralisiert sind und lediglich Hydroniumionen aus dem Ionenprodukt des Wassers den pH-Wert bestimmen. Bei basischen/sauren Salze käme eine zusätzliche pH-Wertverschiebung hinzu, die jedoch bei dem hier gebildeten Natriumchlorid nicht berücksichtigt werden muss.
Schwieriger wird es mit den Zwischenwerten, bzw. auch den nachfolgenden Werten.
Werte zwischen pH=1 und pH=7 (rot):
Um den pH-Wert berechnen zu können, brauchen wir die aktuelle Konzentration an Hydroniumionen nach jedem Zusatz von Natronlauge. Um diese Konzentration zu bestimmen, benötigen wir jeweils eine Stoffmenge n und ein Volumen V, da ja gilt:
c(H3O+)=n(H3O+)/V(Lösung)
Vereinfachend setzen wir voraus, dass die Natronlauge in 1mL-Schritten zugesetzt wird. Vorhanden sind ja schon V0=10mL Probelösung (Salzsäure). V0 sei unser Startvolumen. Mit jedem Zusatz von 1mL Natronlauge kommt somit 1mL Flüssigkeit hinzu. Nach dem ersten Zusatz von 1mL Natronlauge gilt also für das Volumen (V1):
V1=V0+1*1mL
Für beliebige Zusätze n, die in 1mL-Schritten erfolgen gilt dann:
Vn=V0+n*1mL
Das ging ja noch. Die Übersetzung dieses ganzen Kauderwelsch heißt also einfach: Nach jedem Zusatz von 1mL erhöht sich das Volumen um 1mL. Logisch.
Bei der Stoffmenge n wird es nur wenig schwieriger. Auch hier brauchen wir ein n0, also die Stoffmenge an Hydroniumionen zu Beginn der Titration.Das ist nicht weiter schwer, da bekannt ist:
V(HCl)=10mL=0,01L
c(HCl)=0,1mol/L
mit c=n/V bzw. n=c*V ergibt sich für n0:
n0=c(HCl)*V(HCl)=0,1mol/L*0,01L=0,001mol
Nach jeden Zusatz von Natronlauge verringert sich die Stoffmenge an Hydroniumionen um die in der Natronlauge enthaltene Stoffmenge an Hydroxidionen, da gemaß
H3O+ + Cl- + Na+ + OH- ==> 2H2O + Na+ + Cl-
ein Hydroniumion durch ein Hydroxidion neutralisiert wird.
In 1mL Natronlauge der Konzentration c(NaOH)=0,1mol/L sind mit
V(Natronlauge)=1mL=0,001L
c(NaOH)=0,1mol/L
gemäß c=n/V bzw. n=c*V
n(NaOH)=c(NaOH)*V(Natronlauge)=0,1mol/L*0,001L=0,0001mol
Hydroxidionen enthalten.
Die Stoffmenge an Hydroniumionen verringert sich also mit jedem Zusatz von 1mL Natronlauge um 0,0001mol. Damit gilt analog zum Volumen:
nn(HCl)l=n0(HCl)-n*0,0001mol
Damit kann ich für die Zugabe von 1–9mL Natronlauge V(H3O+) und n(H3O+) bestimmen.
Werte ab pH7 (blau):
Von n0=0,001mol kann ich nur 10x 0,0001mol abziehen. Danach werden die Werte negativ und somit sinnbefreit. Eine Bestimmung der Konzentration an Hydroniumionen über diesen Punkt hinaus erscheint auf den ersten Blick aussichtslos. Glücklicherweise sind pH und pOH über das Ionenprodukt des Wassers miteinander verknüpft, (s.o.) d.h. ich kann bei verdünnten Lösungen aus der Konzentration der Hydroxidionen auf die Konzentrration der Hydroniumionen schließen.
Bei jeden Zusatz von Natronlauge über den Äquivalenzpunkt hinaus erhöht sich die Stoffmenge an Hydroxidionen, da ja alle Hydroniumionen aus der Protolyse der Säure neutralisiert sind, d.h. die Stoffmenge n an Hydroxidionen nimmt mit jedem Zusatz von 1mL Natronlauge um
n=0,0001mol
zu. Das Volumen steigt pro Schritt weiter um 1mL. Damit kann ich c(OH-) bestimmen, daraus pOH ableiten. pH bekomme ich dann via:
pKw=pH+pOH bzw. pH=pKw-pOH bzw. pH=14-pOH
doch indirekt zum pH-Wert.
Und jetzt die ganze Rechnung/Auswertung:
Am besten nimmt man dafür eine Tabellenkalkulation oder das Tabellenblatt eines Taschenrechners. Dann kommt z.B. sowas dabei heraus:
| Verbrauch an Natronlauge [mL] | V [L] | n(H3O+) bzw. n(OH-) [mol] | c(H3O+) bzw. c(OH-) [mol/L] | pH |
| 0 | 0,010 | 0,0010 | 0,100000 | 1 |
| 1 | 0,011 | 0,0009 | 0,081818 | 1,09 |
| 2 | 0,012 | 0,0008 | 0,066667 | 1,18 |
| 3 | 0,013 | 0,0007 | 0,053846 | 1,27 |
| 4 | 0,014 | 0,0006 | 0,042857 | 1,37 |
| 5 | 0,015 | 0,0005 | 0,033333 | 1,48 |
| 6 | 0,016 | 0,0004 | 0,025000 | 1,6 |
| 7 | 0,017 | 0,0003 | 0,017647 | 1,75 |
| 8 | 0,018 | 0,0002 | 0,011111 | 1,95 |
| 9 | 0,019 | 0,0001 | 0,005263 | 2,28 |
| 10 | 0,020 | 0,0000 | 0 | 7 |
| 11 | 0,021 | 0,0001 | 0,004762 | 11,68 |
| 12 | 0,022 | 0,0002 | 0,009091 | 11,96 |
| 13 | 0,023 | 0,0003 | 0,013043 | 12,12 |
| 14 | 0,024 | 0,0004 | 0,016667 | 12,22 |
| 15 | 0,025 | 0,0005 | 0,020000 | 12,3 |
| 16 | 0,026 | 0,0006 | 0,023077 | 12,36 |
| 17 | 0,027 | 0,0007 | 0,025926 | 12,41 |
| 18 | 0,028 | 0,0008 | 0,028571 | 12,46 |
| 19 | 0,029 | 0,0009 | 0,031034 | 12,49 |
| 20 | 0,030 | 0,0010 | 0,033333 | 12,52 |
Oder als Diagramm:
Tja – ich hoffe, das stimmt jetzt alles so…
Kritische SuS werden sagen, dass bei pH7 ja immer noch Hydroniumionen vorhanden sind, d.h. gar nicht alle Hydroniumionen neutralisiert sind – deswegen klappt die Rechnung für pH=7 ja auch nicht. Da muss ich nochmal drüber nachdenken. Außerdem wäre es eine gute Idee, im Bereich um pH7 herum die Volumenzugabe von Natronlauge stark zu reduzieren (etwa 0,1mL), um bessere Werte zu erhalten – dank Tabellenkalkulation ja prinzipiell kein Problem.


Bei jeden Zusatz von Natronlauge über den Äquivalenzpunkt hinaus erhöht sich die Stoffmenge an Hydroxidionen, da ja alle Hydroniumionen aus der Protolyse der Säure neutralisiert sind, d.h. die Stoffmenge n an Hydroxidionen nimmt mit jedem Zusatz von 1mL Natronlauge um.
Wenn du diesen ausgebesserten Satz einfügst, dann stimmt alles. Die Rechnung bei pH=7 funktioniert natürlich. Allerdings eben nur, wenn man im Hinterkopf behält, dass lediglich die zusätzlichen Hydroniumionen aus der Protolyse der Säure wegneutralisiert wurden. Schon sind wir wieder beim pH von reinem Wasser, in diesem Falle allerdings mit darin gelösten Natrium- und Chlorid-Ionen.
Was meinst dazu?
Grüße
DR
Danke für die zusätzlichen Hinweise! Ich habe sie gleich eingearbeitet. Wenn das so weiter geht, kann dieser Artikel bald bei Wikipedia referenziert werden :o)…
Gruß,
Maik
Außerdem musst du die Autoprotolyse des Wasser berücksichtigen, die Na+ und Cloridionen kannst du vernachlässigen, weil die weder Base noch säre sind, also pH-neutral sind
Liebe Grüße
Kristina
* Säure
Naja, die Konzentrationen der Autoprotolyse (oder auch das MGW daraus) kann bei den Konzentrationen für Säure / Lauge vernachlässigt werden. Im Prinzip zwar falsch, aber wenn es nicht gemessen werden kann, vereinfacht es dich Rechnung stark. Leztendlich wird bei ph + pOH =7 ja auch die Konzentration des Wassers in sich selbst (s. mwg) nicht beachtet, auch wenn sich diese im Prinzip minimal ändert.
das hat mir echt weitergeholfen,aber wie funkitoniert das ganze wenn die titration umgekehrt abläuft? Also 0,1 m naoh mit 1 m hcl titriert wird? Ich habe versucht das nach dem schema zu rechnen,aber so ganz funktioniert das nicht, weil der ph steigt und doch eigentlich sinken sollte, oder nicht?
Kann mir da vielleicht jemand helfen? Das wäre echt super :)
ps: Dass ich die erhaltenen und zum pOH logaritmiereten C‑werte von 14 abziehen muss ist mir bewuss :D
kann mir da BITTE jemand weiterhelfen?
danke :)
lg katja
Poste mal eine deiner Zwischenrechnungen zwischen c(OH-)=0,1 (pOH=1) und c(OH-)=7 (pOH)=7 mit eingesetzten Zahlenwerten. Deine Maßlösung (1mol/L) ist gegenüber der Probelösung (0,1mol/L) mit zehnfach konzentriert. Vielleicht haut es dich da raus.
danke für die schnelle Antwort :)
nach 1 ml titration von 1m hcl hab ich mir gedacht sieht n(naoh) dann so aus:
(0,1m/l*0,101l)- 0,001mol =9,1 *10 hoch ‑3
‑log davon sind 2,040 der ph also 11,96 bis dahin alles gut..
nur sind dann wenn man es so weiterrechnet bei 2 ml hclzugabe der ph 11,964 usw.
Schreib bitte noch einmal die Eckdaten auf, d.h. die Konzentration der Maßlösung und das Volumen der Probelösung.
100 ml 0,1m säure und 20 ml 1m lauge
(0,1m/l*0,101l)- 0,001mol
Die letzte Zahl gibt n(OH) in einem Milliliter Maßlösung an. Das ist ok. n(H+) veringert sich pro Zugabe um diesen Betrag. Wo ist dann die gesamte Stoffmenge von n(H+) in deiner Formel, also das n(0)?
n(aktuell)=n(anfang)-x*n(OH in einem Milliliter)
V(aktuell)=V(anfang)+x*1mL
x = Anzahl der zugesetzten MIlliliter
c(aktuell)=n(aktuell)/V(aktuell)
Ein Milliliter Maßlösung neutralisiert 10mL Probelösung, d.h. bei einem Zusatz von nur 10mL bist du bei pH=7.
no ist 0,01 mol.
Ich habe jetzt alles noch mal durchgerechnet und komme auf Ergebnisse,die für mich logisch sind. Danke :)
Vielen Dank für die genaue Durchführung, Sie haben mir sehr geholfen.
„Kritische SuS werden sagen, dass bei pH7 ja immer noch Hydroniumionen vorhanden sind, d.h. gar nicht alle Hydroniumionen neutralisiert sind – deswegen klappt die Rechnung für pH=7 ja auch nicht.“
Na ja, wenn man an dieser Stelle – je nach Jahrgangsstufe – das Ionenprodukt des Wassers einfließen lässt (natürlich gleich mit Verhältnismäßigkeit wie torsten sie beschrieben hat, damit das bei den anderen Berechnungen nicht unnötig schwierig wird), dann kann man auch den pH-Wert nach Zugabe der Hälfte berechnen.
Hallo,
mir wurde die Frage gestellt, „warum man bei der Titrationskurve den pH-Wert 14 nicht erreicht, obwohl wir doch mit 1 molarer Natronlauge titriert haben?“ Die Maßlösung war eine 0,1 molare Salzsäure, 100 ml.
Wie komme ich hier zu einer überzeugenden Erklärung?
Die pH-Skala ist logarithmisch. Deine Probelösung, die du neutralisierst, verdünnt dir deine Maßlösung. Da kannst du bis zum St. Nimmerleinstag titrieren, um auf pH14 zu kommen, schon allerkleinste Verdünnungen haben erheblichen Einfluss auf den pH-Wert – das ist die einfache Antwort. Rechne doch mal durch mit z.B. 1000L deiner Natronlauge + deine 200mL neutralisierte Probelösung – oder mach‘ mit Excel ein schickes Diagramm.
Bei 1mol/L darfst du schon längst nicht mehr mit Konzentrationen rechnen, sondern musst Aktivitäten zugrundelegen. Würde mich nicht wundern, wenn Natronlauge mit c=1mol/L von Natur aus schon gar nicht pH14 hat … Müsste man mal rechnen. Das wäre die für deine Lehrkraft beeindruckende Antwort.
Danke, das hat sehr geholfen!