Das Ionenprodukt des Wassers
Vorbemerkung:
Alle Formeln in diesem Artikel wurden mit diesem Onlinetool erstellt!
Und jetzt los:
Nach langer Zeit kommt hier endlich wieder etwas Fachliches. Mich nerven seit Jahren Lehrbücher mit einem Satz, der immer wieder in der einen oder anderen Form auftritt. Er lautet:
Wie man leicht sieht…
Entweder ich gehöre nicht zur Spezies „man“, ich bin unbegabt oder einfach zu kritisch. Ich sehe zumindest in den seltensten Fällen die ausgelassenen Zusammenhänge „leicht“. Ein prima Beispiel ist der Kw- bzw. pKw-Wert, also das Ionenprodukt des Wassers. Die meisten Lehrbücher machen das so (oder ähnlich):
In geringem Maße protolysiert Wasser sich selbst. Darauf ist auch die geringe Leitfähigkeit von reinem Wasser zurückzuführen. Die Reaktion verläuft gemäß:
Für diese Reaktion lässt sich die Massenwirkungskonstante K formulieren:
Und jetzt kommt der Satz:
Wie man leicht sieht, kann die Konzentration des Wasser bei verdünnten sauren und basischen Lösungen als weitere Konstante betrachtet und die Konzentration des Wassers mit in die Massenwirkungskonstante K einbezogen werden, indem man beide Seiten mit dem Term c(H2O)2 multipliziert:
also
Da der Term K * c(H2O)2 jetzt gemäß obiger Voraussetzung ein Produkt zweier Konstanten ist, fasst man beides zu einer neuen Konstante Kw zusammen:
Der Wert von 10-14 mol2/L-2 ergibt sich aus der Tatsache, dass reines Wasser einen pH=Wert von 7 aufweist, dort also gilt c(H3O+) = c(OH-) = 10-7 mol/L. So weit so gut. Aber was geschieht eigentlich, wenn man die reale Konzentration des Wassers mit einbezieht? Wie stark weicht dann Kidealisiert (Annahme: Die Konzentration des Wassers ist konstant) dann von Kreal (die Konzentration des Wassers ist nicht konstant) ab?
Rechnen wir das doch einmal näherungsweise.
Schritt 1: Die Konzentration des Wassers in einem Liter Wasser – oder kurz c0(H2O)
gegeben/bekannt:
Dichte von Wasser bei 25°C (298K): Ï(H2O)298K = 0,997kg/L
Molare Masse des Wassers: M(H2O) = 2*M(H) + 1*M(O) = 2*1g/mol + 1*16g/mol = 18g/mol = 0,018kg/mol
gesucht:
n(H2O)
allg. gilt:
n(H2O) kann berechnet werden, indem man die Dichte des Wasser durch die molare Masse teilt, also n(H2O) = Ï(H2O)298K/M(H2O)
einsetzen:
n(H2O) = 0,997kg/L / 0,018kg/mol ≈ 55,38mol
In einem Liter Wasser sind also ca. 55,38mol Wassermoleküle enthalten, oder anders ausgedrückt:
(1) c0(H2O) = 55,38mol/L
Schritt 2: Kidealisiert berechnen
Der Wert von Kidealisiert bleibt bei jeder erdenklichen Hydronium- bzw. Hydroxidionenkonzentration ja konstant – so die Voraussetzung „Die Konzentration des Wassers ist vernachlässigbar“. Wir nehmen einmal einen pH-Wert von 7, d.h. c(H3O+) = c(OH-) = 10-7 mol/L. So gilt:
Das ist jetzt der Referenzwert (100%), zu dem Abweichungen bestimmt werden. K besitzt keine Einheit, da ja schließlich lediglich ein Verhältnis von umgesetzten zu nicht umgesetzten Wassermolekülen angegeben wird. Es gilt also:
(2) Kidealisiert ≈ 3,26057 * 10-18
Schritt 3: Berechnung von Kreal bei einer Hydroniumkonzentration von c(H3O+) = 0,1 mol/L (verdünnte Lösung)
Dazu geht man vereinfacht von 1 Liter Lösung aus. Wenn in der Lösung 0,1mol (=10-1) Hydroniumionen vorhanden sind, so sind gleichzeitig 10-13mol OH--Ionen vorhanden. Für die tatsächliche Wasserkonzentration c(H2O) gilt dann:
c(H2O) = c0(H2O) – c(H3O+) – c(OH-) = 55,38mol/L – 0,1mol/L – 10-13mol/L ≈ 55,28mol/L
Man mag mir nachsehen, dass ich die Konzentration der Hydroxidionen hier nicht berücksichtigt habe – 10-13 ist für mich eine verdammt kleine Zahl. Für Kreal ergibt sich dann:
Schritt 4: Berechnung von Kreal bei einer Hydroniumkonzentration von c(H3O+) = 1,0 mol/L (konzentrierte Lösung)
Dazu geht man wieder vereinfacht von 1 Liter Lösung aus. Wenn in der Lösung 1mol (=100) Hydroniumionen vorhanden sind, so sind gleichzeitig 10-14mol OH--Ionen vorhanden. Für die tatsächliche Wasserkonzentration c(H2O) gilt dann:
c(H2O) = c0(H2O) – c(H3O+) – c(OH-) = 55,38mol/L – 1mol/L – 10-14mol/L ≈ 54,38mol/L
Auch hier ist die Konzentration der Hydroxidionen zu gering, um rechnerisch wirklichen Niederschlag zu finden. Für Kreal ergibt sich:
Schritt 5: Bestimmung der jeweiligen Abweichung vom idealisierten Wert
Dazu nehme ich folgende Formel:
Kabweichung= 1-(Kreal/Kidealisiert)*100
Für die verdünnte Lösung ergibt sich:
Kabweichung ≈ 0,3%
Für die konzentrierte Lösung hingegen:
Kabweichung ≈ 3,5%
Ich bin kein guter Fehlerrechner, aber rein logisch müssten die berechneten Abweichungen durchschlagen auf den Kw-Wert – zumindest in der Relation. Die erste Abweichung dürfte unterhalb der Messgenauigkeit der meisten (Schul-)Messgeräte liegen. Die zweite Abweichung ist schon erheblich. Dennoch wird teilweise in der Literatur für Lösungen bis 1mol/L mit der idealisierten Gleichung gerechnet. Nunja. Es ist eben mühsam sich mit Aktivitäten und Tabellenwerken herumzuschlagen.
Wie man leicht sieht, ergeben sich aus derartigen Fragestellungen:
- Hervorragende Einsatzmöglichkeiten für einen in der Mathematik eingeführten grafikfähigen Taschenrechner
- Hervorragende Möglichkeiten, um problemorientiertes Denken zu schulen, Welt zu hinterfragen
- Eine didaktische Brücke zur Einführung des Aktivitätsbegriffes (was in der Schule ja aber nach Meinung mancher Curriculaverfasser „viel zu schwer“ ist – selbst im LK)
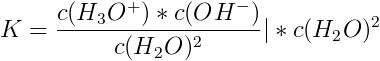
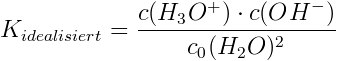
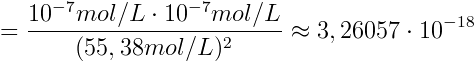

Pingback: Titrationskurve berechnen - riecken.de - Gedanken zu Bildung, Lehre und Schule
Sehr geehrte Damen und Herren !
Danke für die verständliche Darstellung und die Zahlenbeispiele.
Im 74. Lebensjahr hab ich es nun kapiert.
Kw = 1,0 * 10^-14 (mol/l)^2 und nicht 14
wie jate schon angemerkt hat
Kw= 10^-14 und nicht 14
PKs + PKb ist 14 aber nicht Kw
Wie die meisten schon angemerkt haben Kw=10^-14 !!!
Völlig richtig. Nach 10 Jahren habe ich das jetzt mal angepasst …
Ein riesiges Dankeschön für diesen Beitrag – endlich mal jemand, der diese Selbstverständlichkeit hinterfragt und auch noch aufklärt!