Strukturformeln – Abstraction layer
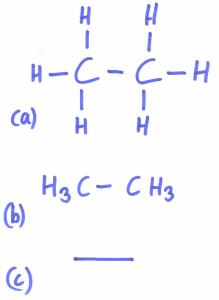
In der organischen Chemie nutzen wir im Unterricht Strukturformeln zur symbolischen Darstellung von Molekülen. Das kann man auf recht unterschiedlichem Abstraktionsniveau tun (hier am Beispiel des Ethans):
(a) ist ein Beispiel für eine vollständige Strukturformeln. Mit etwa Übung schafft man es, die Wasserstoffatomrümpfe an der Tafel in einem Rhythmus zu schreiben. Bei längeren Kohlenwasserstoffketten oder gar verzweigten nervt das nur noch. Daher besteht unter Chemielehrern die pragmatische, aber völlig IUPAC-widrige Vorgehensweise, die Wasserstoffatomrümpfe einfach wegzulassen. Laut IUPAC steht nämlich ein offenes Strichende stets für eine Methylgruppe…
(b) ist ein Kompromiss aus Summen- und Strukturformel, gemeinhin als Halbstrukturformel bekannt. Das ist ein IUPAC-konformer und praktikabler Ausweg aus der der Misere bei den Strukturformeln.
© Ist eine Skelettformel. Ein Strichende steht für eine Methylgruppe, eine (hier optionale) Ecke für eine CH2-Gruppe. Chemiker sind schreibfaul. Deswegen hat man so etwas erfunden. Wir Chemielehrer nutzen das z.B. bei größeren Molekülen (etwa Fetten), Biologen tun das (die können sich nicht mit kleinen Moleküle bescheiden), Schulbücher tun es, Wikipedia sowieso – weil es eben so schön fluffig zu schreiben ist.
Selten erleben ich es, dass man Skelettformeln SuS systematisch beibringt, dabei ist die Welt voll davon. „Zu abstrakt im OC-Anfangsunterricht“ – ein häufiges Argument. Man kann sich mit dieser Abstraktion jedoch eine Menge Zeit sparen und so ein Thema wie die Nomenklatur der Alkane hübsch in eine Geschichte verpacken – in die Geschichte von den Gliedertieren.
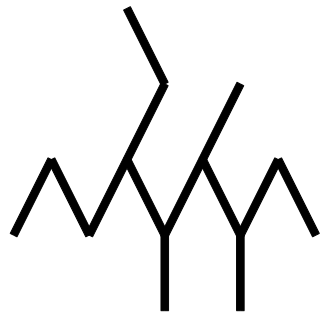
Hier ist ein solches und sucht nach seinem Namen:
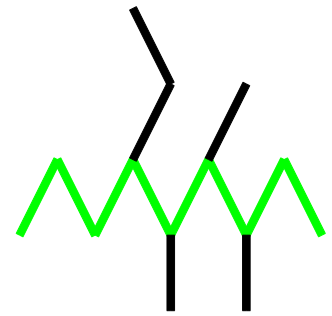
Zuerst suchen wir die längste Gliederkette:
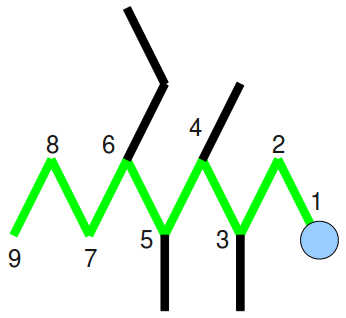
Dann nummerieren wir sie so durch, dass die Anhängsel möglichst kleine Zahlen erhalten und malen dem Tier einen Kopf am ersten Kohlenstoffatomrumpf oder eben möglichst nahe an den meisten Extremitäten:
Unser Tierchen besitzt neun Kohlenstoffatomrümpfe (Nonan). Jetzt schauen wir uns die Extremitäten des Tieres genauer an:
Wir haben dreimal einen einfachen Strich als Extremität, also drei Meythylgruppen, die an den Gliedern 3,4, und 5 sitzen (3,4,5‑trimethyl-). Der Strich mit Knick am 6. Glied ist eine Ethylgruppe (6‑ethyl-).
Name:
6‑Ethyl‑3,4,5‑trimethylnonan
Wenn die Skelettformelschreibweise sauber eingeführt und durch Transformationsübungen eingeschliffen ist, werden die SuS schon sehr früh die Molekülwelt auf Wikipedia und anderswo sofort verstehen. Bei der Nomenklatur spart man sich viel Tafelgeschreibsel. Bei mir hat es prima geklappt. Jetzt malen sie zwar immer Tierchen, aber wenn der Name hinterher stimmt, dann hilft diese Abstraktion sehr.