Allgemeines Gasgesetz und Diagramme
Das allgemeine Gasgesetz braucht man in der Schule oft in Zusammenhang mit dem Satz von Avogadro. Es stellt einen Zusammenhang zwischen Druck, Volumen, Teilchenanzahl und Temperatur eines Gases her, berücksichtigt jedoch weder mögliche Anziehungskräfte zwischen Gasteilchen, noch Abweichungen der Gasteilchen von der Kugelform. Trotzdem bildet es eine gute Näherung für viele „Alltagsgase“ und reicht für schulische Zwecke vollkommen aus.
![]()
Bedeutung der einzelnen Größen:
p: Druck in [kPa]1
V: Volumen in [L]
n: Stoffmenge („Teilchenanzahl“) in [mol]
R: allgemeine Gaskonstante
![]()
T: Thermodynamische Temperatur [K]
1 In der Schule rechnet man gerne in hPa, weil das besser zu der vormals gebräuchlichen Einheit mbar passt.
Exkurs – die Einheiten:
Damit der Term bei Umformung auch immer hübsch in sich zusammenfällt, braucht es etwas Wissen um die Zusammensetzung der Einheiten. Dabei gilt:
… dann passt es später wieder alles.
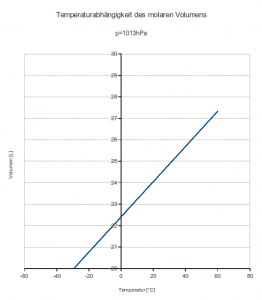
Mit Hilfe dieses Gesetzes lassen sich Diagramme („Visualisierungen“) mit einer Tabellenkalkulation erstellen. Neulich habe ich in unserem Schulbuch diese Darstellung entdeckt (aus rechtlichen Gründen analog nachgestellt):
Mit der nach V umgestellten Gleichung (1) und p = 101,3kPa (1013 hPa) sowie n=1 kann man mit einer Tabellenkalkulation sowas sehr schnell selbst machen.
![]()
Das Diagramm ist trotzdem eine didaktisch lieb gemeinte Katastrophe und eines Bankenverkaufsprospekts würdig.
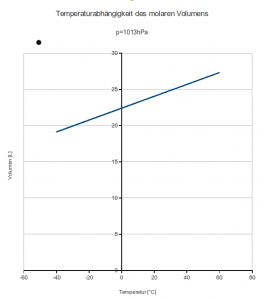
Wer sieht es? Genau. Die y‑Achse wurde beschnitten (oder die x‑Achse verschoben). Das kann man machen, sollte es jedoch im Diagramm kennzeichnen. Macht man es „richtig“, schaut es so aus:
Die didaktischen Reduzierer aus dem Schulbuch mussten noch eine graphische Extrapolationsaufgabe stellen, um klarzumachen, dass die Gerade überhaupt an einer bestimmten bzw. für sie „gewollten“ Stelle die x‑Achse schneidet (-273°C).
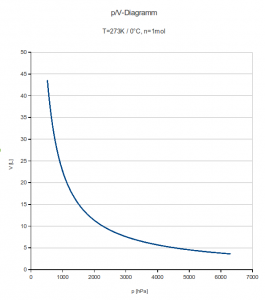
Das kann man mit dem „richtigen“ Diagramm auch noch machen, sieht aber auch vorher viel leichter, dass vor dem Schnittpunkt der Geraden mit der x‑Achse das Volumen negativ wird – bis zur Einführung der thermodynamischen Temperatur ist es dann kein großer Schritt mehr. Ist das geschafft, kann man auch solche Diagramme von SuS beschreiben lassen:
- Beschreibe den Verlauf der Kurve. Erkläre ihn mit dem Kugelteilchenmodell.
- Stelle Vermutungen darüber an, wie die Kurve sich bei noch höheren, bzw. noch niedrigeren Werten für p entwickeln wird.
- Die Kurve wird niemals die x- oder y‑Achse erreichen. Begründe, warum diese Aussage korrekt ist.
Für denjenigen, den es interessiert, hier noch das Tabellenblatt, welches ich für die Berechnung der Diagramme genutzt habe (quick & dirty): ODS | XLS