Ich unterrichte in diesem Schuljahr einen sogenannten polyvalenten Chemiekurs. Dieser Kurs ist notwendig, damit die Schülerinnen und Schüler ihre Belegungspflichten in der Profiloberstufe erfüllen, und er soll prinzipiell fachübergreifend innerhalb der Naturwissenschaften angelegt sein. Als Chemie-/Deutschlehrer tut man sich da selbstredend schwerer als jemand mit einer zweiten Naturwissenschaft als Beifach.
Da ich ja immer fixe Ideen habe (es gibt zu diesem Kurs kein Curriculum!) und es an unserer Schule schon Projekte gab, in denen Schülerinnen und Schüler Grundschülern die Chemie nähergebracht haben, habe ich dem Kurs vorgeschlagen, einen Schritt weiterzugehen und den örtlichen Waldkindergarten mit einzubinden, zu dem ich gute Kontakte haben und die beim Haus der kleinen Forscher mitmachen. Mein Kurs wollte und hat unter dem Rahmenthema „Farben“ einige Experimente ersonnen, aber gleichzeitig auch eine Didaktisierung für Kinder dieses Alters.
Schritt 1 – Planungsphase A:
Anhand von Material aus unserer Schule, z.B. den vom Kurs des letzten Jahres erstellten Reader für die Grundschüler, und anhand von Internetrecherchen wurden verschiedene Versuche von den sechs Teams ausgewählt. Schwerpunkt bildete dabei die Praxis – d.h. es musste Sicherheit um Umgang mit Geräten und Stoffen erworben werden. Ich habe mich nur bei wirklich sicherheitsrelevanten Aspekten eingeschaltet. Hier eine Auswahl von Aufbauten – die Fotos sind von den SuS erstellt (der erfahrene Chemielehrer erkennt einige Klassiker, alle anderen seien auf das Dokumentationswiki verwiesen, welches wir im Kurs gerade befüllen – Link folgt):

Milchbild – Mit Zauberstab und Lebensmittelfarbe Muster zeichnen


Eine einfache Lavalampe – Salz reißt Öl mit…

Schritt 2 – Erprobungphase:
Alle Versuche wurden im Unterrichtsraum an Stationen aufgebaut. Wir sind als ganze Lerngruppe von Station zu Station gezogen. Die zuständigen Teams haben SuS, die die Kinder „simulieren“ sollten, ihren Versuch vorgestellt bzw. durchführen lassen. In dieser Phase kam es auch zu spannenden Erkenntnissen auf beiden Seiten.
Schritt 3 – Planungsphase B:
Die Experimente wurde entsprechend der Erfahrungen (SuS geben erstaunlich realistische Kindergartenkinder ab, wenn man sie nur lässt…) vor allem unter diesen Fragestellungen überarbeitet:
- Was kann ein Kind machen, was ich bisher vorgemacht habe?
- Was kann alles schiefgehen und vermeide ich das durch einen geeigneten Versuchsaufbau?
- Wie setze ich meinen Anspruch an die Vermittlung von Hintergründen zum Experiment kindgerecht um?
- Was brauche ich noch für mein Vorhaben (Material, Hilfen)?
Schritt 4 – Durchführung:
Am 6. Mai war es dann soweit. Die SuS waren für das Projekt für die ersten beiden Stunden nebst Herrn Riecken freigestellt (in der 3./4. Stunde lag unser regulärer Unterricht). Da ich den Unterricht der KuK achte, gehe ich bei Projekten möglichst minimalstundenplaninvasiv vor. Meine regulären Klassen hatten zumindest zur Hälfte Aufgaben erhalten – gleichwohl wurde ich natürlich vertreten. Leider kann ich aus Datenschutzgründen keine Fotos veröffentlichen.
Ich habe selten so beteiligte und engagierte SuS erlebt – selbst Klogänge mit den Kindern wurden selbstbestimmt durchgeführt. Als ein Glückgriff erwies sich, dass Herr Riecken in der Aufregung die Kinder in fünf Gruppen statt in die notwendigen sechs aufgeteilt hatte – so blieb ein „Joker“ und es durfte an Station A auch einmal länger als an Station B dauern.
Schritt 5 – Reflexion:
Erstmal haben wir ca. 200 Fotos von diesem Tag am Beamer geschaut – die Erzieherinnen und Herr Riecken haben viel fotografiert… Dann ging es in den PC-Raum zu einem anonymen Feedback mit Moodle. Hier einige Ergebnisse, die für sich selbst sprechen:
Freitextfrage: Was hat mich bei der Durchführung positiv überrascht?
Kinder waren sehr engagiert.
Das Wissen das einige Kinder bereits mitbringen
Es war alles gut
Die Begeisterung der Kinder sowie die Ausdauer in Bezug auf diese.
Die Kinder waren sehr interessiert und haben viel nachgefragt. Zudem wollten sie viel selbst machen.
Meine eigene, und die Motivation der anderen
Kinder haben die Theorie oft schnell verstanden.
Das überaus starke Interesse der Kinder
nichts
einige Kindergartenkinder waren interessiert und wissbegierig.
Des Weiteren hatten einige der Kids viel Spaß.
Dass die Kinder teilweise gut mitgearbeitet haben und schon einiges verstanden haben
Die meisten Kids waren sehr engagiert dabei!
Wir haben übrigens sehr viel mit dem Kugelteilchenmodell gearbeitet. Das ist – auf jeder Chemiefortbildung zu hören – „wissenschaftlich nachgewiesen“ für Kinder bis zur 6. Klasse „viel zu abstrakt“ – Phänomene reichen aus. In der Physik hingegen ist es „wissenschaftlich erwiesen“, dass es in der 5. Klasse eingesetzt werden sollte, um Phänomene zu erklären, damit es nicht allein auf konsumierendes Gepütscher hinausläuft. Ich oute mich ja immer auf Chemiefortbildungen damit, nicht auf dem neuesten Stand der Wissenschaft zu sein. Die Frage nach Belegen reicht meist aber schon für eine entlarvende „Weilnunmaldasistnunmalso“-Argumentation, meist gepaart mit einem persönlichen Angriff – das nur am Rande.
Weiter mit den Evaluationsergebnissen:
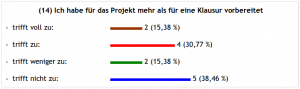
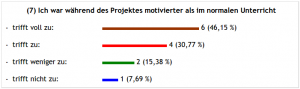
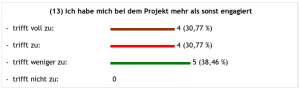
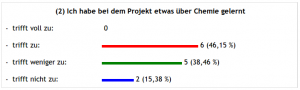
Über den letzten Punkt kann man sich streiten – oder auch nicht, denn:
Freitextfrage: Folgendes würde ich bei einer Wiederholung des Projektes anders machen
eventuell einen anderen Versuch wählen
die Kinder mehr machen lassen.
einfachere Themen, die nicht chemisch erläutert werden müssen und vielleicht noch verständlicher sind.
Ich würde versuchen das Projekt noch strukturierter auszuführen
ein wenig mehr Zeit einplanen
gemeinsame Pause mit den Kindern
Eine längere Zeitspanne auswählen und Versuche wählen die ca. gleich lange Zeit benötigen.
Ich glaube, es wäre sinnvoll das Erklärungsmodell noch besser auf die Kids abzustimmen.
Experimente die die Kinder mehr begeistern
mehr Zeit in einzelne Versuche investieren
Im Anschluss habe ich verschiedene Tools für die Dokumentation der Ergebnisse/Erkenntnisse vorgestellt (Blog, Mahara, GoogleDocs, Wiki) – die Wahl fiel auf ein Wiki.
Schritt 6 – Dokumentation:
Zur Zeit gestalten wir gerade das Wiki – eine für mich und die SuS völlig neue Erfahrung, da wir alle noch nie mit so einem Tool gearbeitet haben – bisher war alles eher WYSIWYG. Wie gesagt – vielleicht verlinke ich es hier, wenn es fertig ist.
Fazit:
Das Projekt läuft ja noch – ich teile die Wahrnehmung vieler SuS nicht, dass wenig über Chemie gelernt wurde. Anhand der Fragen, die in der Vorbereitungsphase gestellt worden sind, konnte ich im Beratungsprozess erkennen, dass da schon das eine oder andere geschehen ist, da fielen schon harte Fachbegriffe wie mobile oder stationäre Phase, Adhäsion usw..
Neben dem ganzen fachlichen Kram war es für mich eine Offenbarung, SuS weitgehend außerhalb systemisch vorgegebener Schülerrollen zu erleben, nämlich z.B. als zugewandte Lernbegleiter oder auch kompetente und umsichtige Experimentatoren, als authentisch neugierig Fragende, als „Wissen-Wollende“. Dafür sind Kinder aber auch sehr effiziente Induzierer… Viel effizienter als vielleicht Menschen mit vorhandener „classic“ Schulerfahrung.
Ich weiß nicht, wie oft zwischen Sammlung und Unterrichtsraum hin- und hergerannt bin, um etwas zu holen, vorzuschlagen, zu beraten, Möglichkeiten aufzuzeigen, zu korrigieren, nachzufragen… . Das war Arbeit – aber eine gänzlich andere, ziemlich fordernde. Der Aufwand „drumherum“ hielt sich in Grenzen, da das Material, was nicht in der Schule vorhanden war, von den SuS besorgt wurde. Ich musste nur Quittungen abrechnen.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ (15)\; K=\frac{c(MnO_{4(aq)})^- \cdot c(H^+)^8}{c(Mn_{(aq)}^{2+})} \]](https://www.riecken.de/wp-content/ql-cache/quicklatex.com-99846cf46da71debae632cdd44933756_l3.png)
![]()
![Rendered by QuickLaTeX.com \[ + \frac{0,059V}{5}\cdot lg \left( \frac{c(MnO_{4(aq)})^- \cdot c(H^+)^8}{c(Mn_{(aq)}^{2+})} \right) \]](https://www.riecken.de/wp-content/ql-cache/quicklatex.com-81cd01a0dbfc1e09cc37b0da3985850f_l3.png)








