Chemieunterricht « Categories « riecken.de

Chemie: Fotometrie mit Kaliumpermanganatlösung

26. Januar 2010 Maik Riecken 4 Kommentare

Es gibt Geräte in der Chemiesammlung, um die man als Lehrer einen ehrfurchtsvollen Bogen macht, z.B. eine Gasmolwaage. Für mich gehörte lange Zeit auch das sündhaft teure Fotometer mit dazu, wir besitzen ein Novaspec II mit seriellem Anschluss. Dummerweise steht in diesem Jahr für den Schwerpunktkurs Chemie auf erhöhtem Niveau hier in Niedersachsen das Lambert-Beersche Gesetz auf dem Zettel, sodass man drei Alternativen hat:

Es als Referat zu vergeben
Es theoretisch durchzukauen – da gibt es im Netz hervorragende Praktikumsberichte
In den sauren Apfel zu beißen und es praktisch zu probieren

Ich habe mich mich für die dritte Option entschieden, auch wenn damit die Verbindliche-Abitur-Vorgaben-Macher es damit geschafft haben, Lehrerfortbildung zum Nulltarif zu evozieren.

Ein Kollege ist am vergangenen Freitag extra länger geblieben, um mich in die Geheimnisse dieses Geräts einzuweihen. Glücklicherweise lässt es sich komplett mit einem Laptop fernsteuern – eine Lizenz für die Software AKAnalytik32.NET gibt es an der Schule auch. Mehr braucht es nicht.

Nach einer theoretischen Einführung der SuS in die Grundlagen der Fotometrie habe ich mich für die Untersuchung von Permanganatlösungen entschieden und das aus mehreren Gründen:

Wässrige Redoxsysteme kann man sowieso nicht genug üben
Kaliumpermanganat lässt sich auch zur Gewässeranalyse trefflich einsetzen zur Bestimmung des Anteil an oxidierbaren Substanzen und unser Haupthema ist die Gewässeranalyse (didaktische Integration/Kombination möglich)
Permanganatlösung haben über eine recht breiten Spektralbereich eine brauchbar hohe Extinktion – da kann man nicht viel falsch machen
Auch sehr niedrigkonzentrierte Lösungen c(KMnO₄) = 0,001mol/L haben schon satt Farbe, woran sich die Empfindlichkeit des Verfahrens zeigen lässt

Die Stunde sah folgendermaßen aus (das Prinzip der Fotometrie war den SuS bereits bekannt):

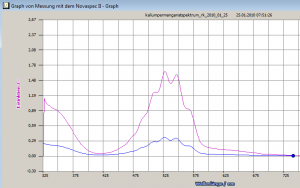
Schritt 1: Aufnahme eines Vollspektrums zur Bestimmung einer geeigneten Wellenlänge für die Messung

Das ist mit der Kappenberg-Software supersimpel. Das Spektrum sah so aus:

Nette Versuche Chemie, Fotometrie, Lambert-Beer, Lösung, Permanganat, Versuch

Organik: Quantitative Analyse

25. Januar 2010 Maik Riecken Kommentar hinterlassen

Eine typische Aufgabe für den Anfang (Kohlenwasserstoffe) könnte so aussehen:

Bei der Verbrennung einer organischen Substanz, die nur aus den Elementen Kohlenstoff und Wasserstoff besteht, werden bei Normalbedingungen 0,63L Kohlenstoffdioxidgas und 0,63g Wasser gebildet. Berechne das Anzahlverhältnis zwischen Kohlenstoff- und Wasserstoffatomen in dieser Verbindung.

Bei dieser Aufgabe ergibt sich im Verlauf der Rechnung ein Problem, welches wir im Chemieunterricht gerne durch eine entsprechende Frisierung der Ausgangsdaten umgehen: Wir bekommen zwei Zahlen mit Rundungsfehlern und müssen darauf ein ganzzahliges Anzahlverhältnis ermitteln, da es nunmal nur ganze Atome gibt. Für das obige Beispiel ergibt sich:

Stoffmenge des Kohlenstoffs

gegeben:

V(CO₂) = 0,63L

V_m(CO₂) = 24L/mol (Satz von Avogadro, Normalbedingungen: 25°C)

gesucht:

n(CO₂)

allg. gilt:

n(CO₂) = V(CO₂) / V_m(CO₂)

einsetzen:

n(CO₂) = 0,63L / 24L/mol â‰ˆ 0,026mol

Stoffmenge des Wassers:

gegeben:

M(H₂O) = 18g/mol

m(H₂O) = 0,63g

gesucht:

n(H₂O)

allg. gilt:

M(H₂O) = m(H₂O) / n(H₂O) â†” n(H₂O) = m(H₂O) / M(H₂O)

einsetzen:

n(H₂O) = 0,63g /18g/mol â‰ˆ 0,035mol

Pro Wassermolekül sind zwei Wasserstoffatome gebunden, sodass für die ursprüngliche Stoffmenge an Wasserstoff der doppelte Wert anzusetzen ist:

n(H) = 2*n(H₂O) = 0,07mol

Das Problem:

Es ergibt sich ein Anzahlverhältnis

n© : n(H) = 0,026 : 0,07 â‰ˆ 0,37

Wie komme ich jetzt auf ein ganzzahliges Anzahlverhältnis? Wie mache ich aus dieser Dezimalzahl wieder einen Bruch und berücksichtige dabei Rundungsfehler?

Ein Mathematikkollege brachte mich auf folgenden Ansatz:

0,37 = n©/n(H) â†” n© = 0,37*n(H)

n© und n(H) sollen dabei möglichst nahe an einer Ganzzahl liegen.

(a) Den Graphen der Funktion zeichnen und schauen, an welcher Stelle dieses Kriterium erfüllt ist

(b) Einfach eine Wertetabelle anlegen, z.B. mit dem Taschenrechner, der bei uns ein Algebrasystem mit an Bord hat:

n(H)	n©
1	0,37
2	0,74
3	1,11
4	1,48
5	1,85
6	2,22
7	2,59
8	2,96
9	3,33
10	3,7

Mit hinreichender Genauigkeit passt das 8. Wertepaar. Es gilt hier also:

n© : n(H) = 3 : 8

So geht es dann doch trotz der recht krummen Werte, denen man das ganzzahlige Verhältnis nicht auf den ersten Blick ansieht. Ok – man kann das auch auf molare Verhältnisse hochrechnen, aber so kommt der TR zum Einsatz und langsamer ist es auch nicht.

Chemieunterricht Analyse, Chemie, Dezimalzahl, Problem, quantitativ, Verhältnis

Sulfatbestimmung – konduktometrisch

10. Januar 2010 Maik Riecken Kommentar hinterlassen

Die Grundidee war nicht schlecht: Man nehme sich ein Mineralwasser mit hohem Sulfatgehalt („Sulfatwässer“ – schmecken bitter) – geeignete Marken finden sich z.B. hier – und achtet darauf, dass die Hintergrundleitfähigkeit nicht zu hoch ist. Die Stoffmenge der Sulfationen muss die der übrigen Ionen am besten weit übersteigen, damit die Hintergrundleitfähigkeit dabei keinen Strich durch die Rechnung macht. Dann lässt sich z.B. mit Bariumchloridlösung gemäß

Ba²⁺ + SO₄^2- → BaSO₄↓

das Sulfat quantitativ fällen. Bariumsulfat hat ein sehr, sehr niedriges Löslichkeitsprodukt und findet daher trotz der hohen Giftigkeit von Bariumionen sogar in der Medizin als Kontrastmittel Anwendung.

Die Stunde sah dann so aus, dass ich mir ein Sulfatwasser mit 1000mg/L Sulfationen besorgt (äh – ich habe auf die Schnelle eines mit Natriumsulfat und Deionat „gebaut“) und mit den SuS gemeinsam die Konzentration der Maßlösung so eingestellt habe, dass der Aquivalenzpunkt so ungefähr bei 25mL Maßlösungsverbrauch liegt – der Sulfatgehalt stand ja auf der „Flasche“. Folgendes Diagramm kam dabei heraus:

Wie Sie sehen, sehen Sie gar nichts (keine zwei Bereiche mit unterschiedlicher Steigung), obwohl doch das Natriumsulfat als einziges gelöstes Salz vorlag – was war dann nur geschehen?

Antwort: Wer schummelt, wird bestraft – bei kleinen Sünden sofort.

Deionat ist in der Regel sauer. Es wurde von mir aber mit der Absicht verwendet, das Problem der Hintergrundleitfähigkeit – wie es beim „echten Mineralwasser“ vorgekommen wäre – auszuschalten. Dummerweise besitzen Hydroniumionen eine beachtliche Äquivalentleitfähigkeit, die die der übrigen Ionen um ein Vielfaches übersteigt. Und da war sie dann wieder, unsere Hintergrundleitfähigkeit. Bariumsulfat ist bei dem Versuch super ausgefallen. Nur hat wahrscheinlich die Hintergrundleitfähigkeit durch die Hydroniumionen die dadurch aufgetretene Veränderung der Lösung quasi „überstrahlt“.

Fazit:

Nicht schummeln, Mineralwasser vor der Analyse immer abkochen, um Kohlensäure zu entfernen und immer vorher auch vermeintlich „idiotensichere“ Setups ausprobieren. Vorher. Und auch keine Ratschläge von Kollegen zur richtigen Schummeltechnik annehmen.

Anekdoten, Nette Versuche Deionat, Fehlschlag, Hintergrundleitfähigkeit, konduktometrisch, Konduktopmetrie, Mineralwasser, Sulfat

Chloridbestimmung nach Mohr

9. Dezember 2009 Maik Riecken 4 Kommentare

Die Chloridbestimmung nach Mohr ist eines der wenigen Beispiele für Fällungstitrationen mit visueller Endpunktbestimmung, das auch in der Schule mit brauchbarer Genauigkeit funktioniert. Einziger Nachteil sind anfallende Chromatlösungen, die ob ihres großen Volumens erst nach dem Eindampfen ihren Weg in die Flasche mit den chromathaltigen Abfällen finden.

Prinzip dieser Titration

Silberchlorid besitzt ein recht kleines Löslichkeitsprodukt: K_L(AgCl) = 1,7*10^-10 mol²/L². In einer gesättigten Silberchloridlösung sind nur sehr wenige Chloridionen enthalten, wie folgende kleine Rechnung zeigt:

gegeben/bekannt:

K_L(AgCl) = 1,7*10^-10 mol²/L²

Weiter gilt bei einer gesättigten Lösung, die ausschließlich Silberchlorid über einem Bodensatz enthält:

(1) c(Ag⁺) = c(Cl^-)

da ja pro Silberion ein Chloridion frei wird. Zusätzliche Silber- oder Chloridionen in der Lösung verschieben das Gleichgewicht zwischen Bodenkörper und Lösung

(2) AgCl_(s) â†” Ag⁺_(aq) + Cl^-_(aq)

lediglich weiter in Richtung des Feststoffes.

gesucht:

c(Ag⁺)

allgemein gilt:

K_L(AgCl) = c(Ag⁺) * c(Cl^-) =1,7*10^-10 mol²/L²

bzw. unter Einbezug von Voraussetzung (1)

K_L(AgCl) = c(Ag⁺) * c(Ag⁺) =1,7*10^-10 mol²/L²

<=> c(Ag⁺)² = K_L

<=> c(Ag⁺) = âˆšK_L

einsetzen:

c(Ag⁺) = âˆš1,7*10^-10 mol²/L² â‰ˆ 1,3*10^-5 mol/L

So viel bleibt also nicht übrig. Damit dürfte die Fällung das Prädikat „quantitativ“ verdienen.

Allgemein, Nette Versuche Beschreibung, Bestimmung, Chemie, Chlorid, Fällung, Mohr, quantitativ, Titration, Versuch

Titrationskurve berechnen

25. Oktober 2009 Maik Riecken 17 Kommentare

Eine an sich einfach klingende Aufgabe, mit der ich letztens in meinem Chemiekurs kläglich gescheitert bin – es war zu früh, es war nicht gut vorbereitet, ich habe den Anspruch der Aufgabe einfach unterschätzt:

Aufgabe:

Berechnen Sie die Titrationskurve der Titration von 10mL Salzsäure der Konzentration c(HCl)=0,1mol/L mit 20mL Natronlauge der Konzentration von c(NaOH)=0,1mol/L. Stellen Sie dazu den pH-Wert der Lösung in Abhängigkeit vom zugegebenen Volumen an Natronlauge dar.

Vorüberlegungen:

Zwei Punkte der Titrationskurve sind relativ einfach zu finden:

Zu Anfang der Titration (0mL Zugabe von Natronlauge) muss der pH-Wert 1 betragen, da ja gilt: pH=-1*lg(c(H₃O⁺))=-1*lg(0,1)=1
Definitionsgemäß ist am Aquivalenzpunkt – also nach Zugabe von 10mL Maßlösung – ein pH-Wert von 7 erreicht, da ja gilt pK_w=pH+pOH=14; c(OH^-)=c(H₃O⁺) am Äquivalenzpunkt (grün), da alle zusätzlichen Hydroniumionen aus der Protolyse der Säure neutralisiert sind und lediglich Hydroniumionen aus dem Ionenprodukt des Wassers den pH-Wert bestimmen. Bei basischen/sauren Salze käme eine zusätzliche pH-Wertverschiebung hinzu, die jedoch bei dem hier gebildeten Natriumchlorid nicht berücksichtigt werden muss.

Schwieriger wird es mit den Zwischenwerten, bzw. auch den nachfolgenden Werten.

Werte zwischen pH=1 und pH=7 (rot):

Um den pH-Wert berechnen zu können, brauchen wir die aktuelle Konzentration an Hydroniumionen nach jedem Zusatz von Natronlauge. Um diese Konzentration zu bestimmen, benötigen wir jeweils eine Stoffmenge n und ein Volumen V, da ja gilt:

c(H₃O⁺)=n(H₃O⁺)/V(Lösung)

Vereinfachend setzen wir voraus, dass die Natronlauge in 1mL-Schritten zugesetzt wird. Vorhanden sind ja schon V₀=10mL Probelösung (Salzsäure). V₀ sei unser Startvolumen. Mit jedem Zusatz von 1mL Natronlauge kommt somit 1mL Flüssigkeit hinzu. Nach dem ersten Zusatz von 1mL Natronlauge gilt also für das Volumen (V₁):

V₁=V₀+1*1mL

Für beliebige Zusätze n, die in 1mL-Schritten erfolgen gilt dann:

V_n=V₀+n*1mL

Das ging ja noch. Die Übersetzung dieses ganzen Kauderwelsch heißt also einfach: Nach jedem Zusatz von 1mL erhöht sich das Volumen um 1mL. Logisch.

Bei der Stoffmenge n wird es nur wenig schwieriger. Auch hier brauchen wir ein n₀, also die Stoffmenge an Hydroniumionen zu Beginn der Titration.Das ist nicht weiter schwer, da bekannt ist:

V(HCl)=10mL=0,01L

c(HCl)=0,1mol/L

mit c=n/V bzw. n=c*V ergibt sich für n₀:

n₀=c(HCl)*V(HCl)=0,1mol/L*0,01L=0,001mol

Nach jeden Zusatz von Natronlauge verringert sich die Stoffmenge an Hydroniumionen um die in der Natronlauge enthaltene Stoffmenge an Hydroxidionen, da gemaß

H₃O⁺ + Cl^- + Na⁺ + OH^- ==> 2H₂O + Na⁺ + Cl^-

ein Hydroniumion durch ein Hydroxidion neutralisiert wird.

In 1mL Natronlauge der Konzentration c(NaOH)=0,1mol/L sind mit

V(Natronlauge)=1mL=0,001L

c(NaOH)=0,1mol/L

gemäß c=n/V bzw. n=c*V

n(NaOH)=c(NaOH)*V(Natronlauge)=0,1mol/L*0,001L=0,0001mol

Hydroxidionen enthalten.

Die Stoffmenge an Hydroniumionen verringert sich also mit jedem Zusatz von 1mL Natronlauge um 0,0001mol. Damit gilt analog zum Volumen:

n_n(HCl)l=n₀(HCl)-n*0,0001mol

Damit kann ich für die Zugabe von 1–9mL Natronlauge V(H₃O⁺) und n(H₃O⁺) bestimmen.

Chemieunterricht

« 1 … 5 6 7 8 9 … 11 »