Die Faradaysche Konstante bestimmen

Manch­mal bin ich mir selbst so unheim­lich, dass ich gar nicht glau­ben kann, was ich da eigent­lich im Unter­richt mit dem zur Ver­fü­gung ste­hen­den Mate­ri­al mes­se. Von irgend­wo­her habe ich ein Prak­ti­kums­script, in dem die Fara­day­sche Kon­stan­te expe­ri­men­tell mit einem Hoff­mann­schen Zer­set­zungs­ap­pa­rat bestimmt wird. Zunächst aber ein biss­chen Grund­la­gen zum Warmwerden.

Das ers­te Fara­day­sche Gesetz sagt nichts ande­res, als das die bei einer Elek­tro­ly­se abge­schie­de­ne Stoff­men­ge n pro­por­tio­nal zur elek­tri­schen Ladung Q ist, die durch den Ele­kro­ly­ten fließt – mathe­ma­tisch ausgedrückt:

(1) Q ∼ n

Pro­por­tio­na­li­tä­ten haben es so an sich, dass sie über einen Pro­por­tio­na­li­tätfak­tor mit­ein­an­der ver­knüpft sind, im Fal­le des Fara­day­schen Geset­zes gilt hier:

(2) Q = n * z * F

n ist die Stoff­men­ge, z ist die Anzahl der bei der Elek­tro­ly­se pro Ion aus­ge­tausch­ten Elek­tro­nen und F ist Fara­day­sche Kon­stan­te, die wir haben wol­len. z bekom­men wir nahe­zu eli­mi­niert, wenn wir in einem Sys­tem arbei­ten, in dem nur ein Elek­tron aus­ge­tauscht wird, etwa bei der Reduk­ti­on von Protonen:

(3) H⁺ + e^- → H

Mit z = 1 bleibt von Glei­chung (2) nur noch:

(4) Q = n * F oder Q = F * n

Das sieht schon sehr nach einer Gera­den­glei­chung aus:

(5) y = m * x

wobei m die Stei­gung ist. Also muss ich nur Q in Abhän­gig­keit von n bestim­men und die Stei­gung die­ser Gera­den soll­te dann F sein. So der Plan.

In vie­len Ver­suchs­an­lei­tun­gen wird das gra­vi­me­trisch gemacht, d.h. man lagert z.B. einen Fest­stoff an eine Metall­elek­tro­de an, die von Zeit zu Zeit gewo­gen wird, um die Mas­senzu­nah­me zu bestim­men.  Dar­aus lässt sich dann n bestim­men. Das ist aber Stress, da man immer das Lösungs­mit­tel vor dem Wie­gen weg­be­kom­men muss, dabei sowie­so der hal­be müh­sam hin­elek­tro­ly­sier­te Kram abfällt usw.

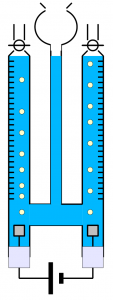
Wenn man aus­schließ­lich mit Gasen arbei­tet und die Stoff­men­ge indi­rekt über das gebil­de­te Gas­vo­lu­men bestimmt, erspart man sich der­ar­ti­ge Pro­ble­me, muss jedoch das Gan­ze als Demons­tra­ti­ons­ver­such fah­ren, da an einer Schu­le kaum mehr als zwei Zer­set­zungs­ap­pa­ra­te  zu fin­den sein werden:

Ich habe als Elek­tro­lyt Schwe­fel­säu­re der Kon­zen­tra­ti­on c=1mol/L ver­wen­det. Als Elek­tro­den­ma­te­ri­al dien­te Pla­tin. Elek­tro­ly­siert wur­de bei kon­stant 0,2A für jeweils zwei Minu­ten. Danach habe ich das Rest­gas aus dem Elek­tro­ly­ten per­len las­sen und das Was­ser­stoff­vo­lu­men bestimmt. Beim Hoff­mann­schen Appa­rat ist es sehr wich­tig, vor dem eigent­li­chen Ver­such bereits etwas Gas zu pro­du­zie­ren, da ansons­ten Feh­ler auf­tre­ten kön­nen – immer­hin ist Sau­er­stoff in Was­ser begrenzt lös­lich (Was­ser­stoff nicht so…), die Elek­tro­den­ober­flä­che muss mit Gas gesät­tigt sein usw.. Die rohen Mess­da­ten sahen so aus:

t [min]	V [mL]
2	2,8
4	6
6	8,9
8	11,9
10	14,8

Erwei­tert man das Gan­ze um die Berech­nung der Ladungs­men­ge Q und die Stoff­men­ge n, die über den Satz von Avo­ga­dro erhält­lich ist, so ergibt sich (man ver­zei­he die Genau­ig­keit, das ist Drag’n Drop aus der Tabellenkalkulation):

t [min]	V [mL]	n(H)	Q [A*s]
2	2,8	0,000233333333333333	24
4	6	0,0005	48
6	8,9	0,000741666666666667	72
8	11,9	0,000991666666666667	96
10	14,8	0,00123333333333333	120

Die Berech­nung von Q ist sehr ein­fach, da gilt:

(6) Q = I * t (Strom in A mul­ti­pli­ziert mit der Zeit in s)

Die Berech­nung von n funk­tio­niert wie bereits gesagt über den Satz von Avo­ga­dro, hier am Bei­spiel der des ers­ten Wertes:

gege­ben:

V=2,8mL=0,0028L

gesucht:

n(Gasteilchen) in V=0,0028L

allg, gilt:

Ein Mol Gas­teil­chen eines idea­len Gases (Was­ser­stoff kommt einem idea­len Gas freund­li­cher­wei­se sehr nahe) nimmt bei einer Tem­pe­ra­tur von T=25°C und eine Druck von 1013hPa ein Volu­men von ca. 24L ein.

Ansatz:

1mol/24L = x mol/V <=> x=V/24 x=0,0028/(1*24)≈0,000116mol

Da damit die Anzahl der Was­ser­stoff­mo­le­kü­le bestimmt wur­de, die je zwei Was­ser­stoff­ato­me ent­hal­ten, beträgt die Anzahl der Was­ser­stoff­ato­me das Dop­pel­te, also

n(H)=2*n(H₂)=2*0,000116mol=0,000232mol

Mit den ande­ren Wer­ten ver­fährt man entsprechend.

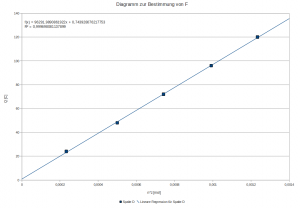
Wenn ich jetzt ein x/y‑Diagramm z.B. mit einer Tabel­len­kal­ku­la­ti­on erstel­le (Q gegen n(H) auf­tra­gen), sieht das so aus:



Die Fara­day­sche Kon­stan­te ist iden­tisch mit der Stei­gung der Gera­den. Wenn man in Open­Of­fice auf das Dia­gramm dop­pelt klickt und dann oben im Menu „ein­fü­gen“ „Trend­li­nie“ => line­ar anwählt, kann man sich die zuge­hö­ri­ge Gera­den­glei­chung und die Feh­ler­qua­dra­te anzei­gen las­sen – die Güte die­ser Gera­den ist schon ver­dammt gut. Jetzt kommt’s:

Mein Ergeb­nis: F = 96292 C/mol

Theo­rie­wert: F = 96485,3 C/mol

Das macht einen Feh­ler von 0,3%. Irgend­was stimmt da nicht… Noch genaue­re Wer­te gibt es, wenn man mit den Gas­ge­set­zen etwa noch den hydro­sta­ti­schen Druck mit berück­sich­tigt, der durch die Was­ser­säu­le ent­steht, die durch das Gas ver­drängt wird. Dabei führt ein klei­ne­res mola­res Volu­men zu noch genaue­ren Wer­ten. Ich muss aber sagen, dass in die­sem Fall mir die Genau­ig­keit für den schu­li­schen Bereich abso­lut reicht… Oder ich hat­te ein­fach nur Schwein…